预训练
DBN中RBM结合方法的缺陷
预训练这一章介绍的是,如何叠加两个RBM,DBN和DBM的不同之处在于如何融合不同的RBM。实际上DBN和DBM的每一层的训练都是一样的,唯一的不同就在于各层训练好之后,如何combine。首先回顾一下RBM,假如现在只有一层,其他层我们都不考虑:
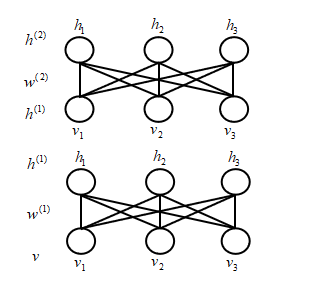
首先,哪些是已知的呢?数据的分布$P_{\text{data}(v)}$是知道的。那么在每一步迭代过程中,可以求出Log-Likelihood梯度,利用对比散度采样(CD-K)算法,就可以把$w^{(1)}$学习出来,而且学习到的$w^{(1)}$还不错,当然这个只是近似的,精确的求不出来,主要原因是后验分布是近似采样得到的。有关RBM的参数学习在“直面配分函数”那章,已经做了详细的描述,这里不再多说了。
我们来表达一下这个模型:
\[\begin{equation} \begin{split} P(v) = & \sum_{h^{(1)}} P(h^{(1)},v) = \sum_{h^{(1)}} P(h^{(1)})P(v|h^{(1)}) \\ = & \sum_{h^{(1)}} P(h^{(1)};w^{(1)})P(v|h^{(1)},w^{(1)}) \\ \end{split} \end{equation}\]其中参数是$w^{(1)}$,为什么呢?因为$P(h^{(1)}) = \sum_v P(v,h)$,而$v$和$h$之间显示是靠$w^{(1)}$来连接的,所以$P(h^{(1)})$一定是和$w^{(1)}$相关的。
第一个RBM求出来以后,那么第二个RBM怎么求呢?实际上这里的$h^{(1)}$都是我们假设出来的。那么下一层RBM连样本都没有,怎么办呢?我们可以将$h^{(1)}$当成是下一个RBM的样本,那么采样得到$h^{(1)}$好采吗?当然简单啦!我们要求的分布为: \(P(h^{(1)}|v;w^{(1)})\) 其中,$v,w^{(1)}$都是已知的,而且由于RBM的良好性质,$h^{(1)}$的节点之间都是相互独立的,那么:
\[\begin{equation} P(h^{(1)}|v;w^{(1)}) = \prod_{i=1}^3 P(h^{(1)}_i|v;w^{(1)}) \end{equation}\]| 而$P(h^{(1)}_i=1 | v;w^{(1)}) = \sigma(\sum_{j=1}^3 w_{ij}v_j)$,而$P(h^{(1)}_i=0 | v;w^{(1)}) = 1 - \sigma(\sum_{j=1}^3 w_{ij}v_j)$,既然概率值我们都算出来了,从0/1分布中采样实在是太简单了。 |
现在,已经将$h^{(1)}$作为下一层RBM的样本,那么怎么构造$h^{(2)}$呢?我们这样构造,
\[P(h^{(1)};w^{(2)}) = \sum_{h^{(2)}}P(h^{(1)},h^{(2)};w^{(2)})\]DBM中把两个RBM简单的挤压成了一个,这个挤压方式很简单,就是用$P(h^{(1)} ; w^{(2)})$来代替$P(h^{(1)};w^{(1)})$,为什么呢?因为,公式(3)的主要难点是要得到$P(h^{(1)})$的概率分布,通过加一层的方式,用第二个RBM来对$P(h^{(1)})$进行建模,这时替换过后$P(h^{(1)})$是和$w^{(2)}$相关了,而公式(3)中是和$w^{(1)}$相关的。这样对$h^{(1)}$进行建模时,只用到了一层的权重。而大家想想真实的$P(h^{(1)})$到底和什么有关,写出来就知道了:
\[P(h^{(1)}) = \sum_{v,h^{(2)}} P(h^{(1)},h^{(2)},v)\]看到这个公式,用屁股想都知道肯定和$w^{(1)}$和$w^{(2)}$都有关。所以,应该表达为$P(h^{(1)};w^{(1)},w^{(2)})$。那么,这样直接压缩的方式是有问题的,DBN采用的就是这种方法(箭头怎么来的,不解释了,“深度信念网络”那一节有详细的解释。),那么DBN中对$h^{(1)}$进行建模时,只用到了一层的权重, 无论用哪一层,肯定是不恰当的。
那么,这样就给了我们一个启示,可不可以同时用到$P(h^{(1)};w^{(1)})$和$P(h^{(1)};w^{(2)})$,对他们两做一个平均,就没有那么极端。简单的处理 就是取一个平均数就可以了。
启发:用$P(h^{(1)};w^{(1)})$和$P(h^{(1)};w^{(2)})$几何平均近似$P(h^{(1)};w^{(1)},w^{(2)})$,这样肯定更加适合,但是怎么平均,是简单的相加除2吗?后续会详细的说明。
Double counting problem
真正要求的是:$P(h^{(1)};w^{(1)},w^{(2)})$。
而目的的直觉是:用$P(h^{(1)};w^{(1)})$和$P(h^{(1)};w^{(2)})$几何平均近似$P(h^{(1)};w^{(1)},w^{(2)})$。
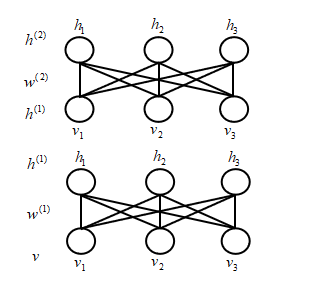
其中,
\[\left\{ \begin{array}{ll} P(h^{(1)};w^{(1)}) = \sum_v P(v, h^{(1)};w^{(1)}) = \sum_v P(v)P( h^{(1)}|v;w^{(1)}) & \\ P(h^{(1)};w^{(2)}) = \sum_{h^{(2)}} P( h^{(1)},h^{(2)};w^{(2)}) = \sum_{h^{(2)}} P(h^{(2)})P( h^{(2)}|h^{(1)};w^{(1)}) \end{array} \right.\]模型中真实存在的只有$v$,而$h^{(1)}$实际上是不存在的,这是我们假设出来的。上一小节讲到了DBN的结合两个RBM的思路中,用$w^{(2)}$来代替$w^{(1)}$,只用到了一层参数。换句话说,只用$P(h^{(1)};w^{(2)})$来近似真实的$P(h^{(1)};w^{(1)},w^{(2)})$,而舍弃了$P(h^{(1)};w^{(1)})$。很自然的可以想到,想要结合$P(h^{(1)};w^{(1)})$和$P(h^{(1)};w^{(2)})$,那么下一个问题就是怎么结合?
| 实际上,$\sum_v P(v)P( h^{(1)} | v;w^{(1)})$这个分布我们是求不出来的。通常是用采样的方法近似求解,假设观测变量集合为:$v\in V, | V | =N$。那么有: |
| 其中,$\frac{1}{N} \sum_{v\in V} P(h^{(1)} | v;w^{(1)})$也被称为Aggregate Posterior(聚合后验),代表着用$N$个样本来代替分布。同样,关于$\sum_{h^{(2)}} P( h^{(1)},h^{(2)};w^{(2)})$可以得到: |
然后,$N$个$h^{(1)}$再根据$w^{(2)}$采样出$N$个$h^{(2)}$,实际上,在learning结束之后,知道$w^{(1)}$和$w^{(2)}$的情况下,采样是很简单的。这样,从底向上采样,就可以计算出各层的后验,合并很简单:
\[\begin{equation} \frac{1}{N} \sum_{v\in V} P(h^{(1)}|v;w^{(1)}) + \frac{1}{N} \sum_{h^{(2)}\in H} P(h^{(2)}|h^{(1)};w^{(2)}) \end{equation}\]即可。这样采样看着倒还是很合理的,那么到底好不好呢?有什么样的问题呢?
这样会导致,Double Counting的问题,也就是重复计算。
假设$V:$是样本集合,$v\in V$;$H:$才是样本集合,$h^{2}\in H$。采样是从下往上依次进行采样,所以,$h^{1},h^{2}$都依赖于$v$。所以,在计算$h^{1},h^{2}$的过程中都用到了$v$相当于把样本利用了两次。那么,重复计算会带来怎样的副作用呢?
下面举一个例子:
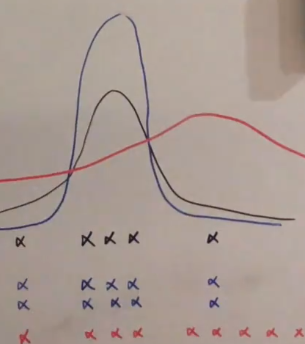
假如红色的是真实分布,我们实际采样得到的是黑色的样本。简单的假设为高斯分布,利用极大似然估计得到黑色的分布。然后不同的利用黑色的样本,从中采样,采样结果重合,不停的重复利用,会导致所表达的分布越来越尖。从而使得偏差很大,所以简单的结合并不行。
预训练总结
上一小节,我们介绍了double counting问题。实际上在玻尔兹曼机这个系列中,我们可以计算的只有RBM,其他版本的玻尔兹曼机我们都搞不定。所以,就想办法可不可以将RBM叠加来得到具有更好的表达能力的RBM模型,于是第一次简单尝试诞生的就是DBN,DBN除了顶层是双向的,其他层都是单向的。中国武学中讲究“任督二脉”,DBN就像只打通了一半,另一半是不通的。很自然,我们想把另外一半也打通,这么模型的表示能力就更强一些。
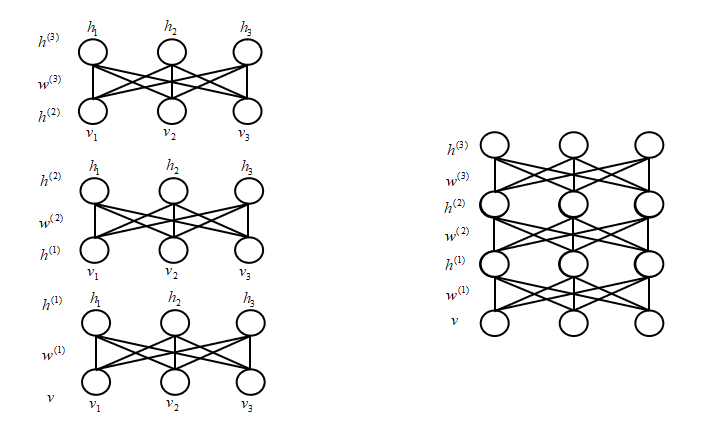
那么,最开始就是将每层RBM的参数$w^{(1)}$,$w^{(2)}$,$w^{(3)}$训练出来之后分别赋予DBM中的$w^{(1)}$,$w^{(2)}$,$w^{(3)}$。但是,这样就会有只用到了一层的参数,所以解决方案是取平均值。比如,在分层的RBM训练中,求的是$2w^{(1)}$,$2w^{(2)}$,$2w^{(3)}$,再将权值$w^{(1)}$,$w^{(2)}$,$w^{(3)}$赋予DBM,相对于每一次只用到了一半的权重。那么,对于中间层$h^{(1)}$来说,就相对于同时用到了$w^{(1)}$,$w^{(2)}$这个在前面,我们已经详细的讲过了。
然而,问题又来了,$v$和$h^{(3)}$只和一层相连。那么,除以2感觉上有一些不对。给出的处理方法是,在RBM的分层学习中,对于$v$从上往下是$w^{(1)}$,从下往上是$2w^{(1)}$,这个问题就解决了。这时不是一个简单的RBM了,我们称之为“RBM”,哈哈哈哈。其近似的概率图模型可以这样认为,来帮助我们理解:
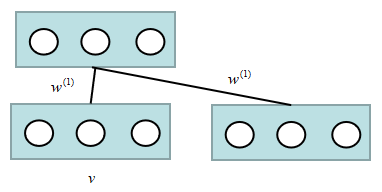
那么,进到$h^{(1)}$有两个$w^{(1)}$,也就是$2w^{(1)}$,而进到$v$只有一个$w^{(1)}$。这就等价于从上往下是$w^{(1)}$,从下往上是$2w^{(1)}$。除了,第一层和最后一层,其他层的都是学习的两倍权值,第一层和最后一层则是“RBM”。
从直觉上看,感觉这一系列演变会让模型的性能越来越好。实际上,可以通过数学证明,DBM的ELBO、比DBN要高,而且DBM的层数越多,每叠加一层RBM,ELBO都会更高。
本章小结
这章中比较完善的讲解了DBM,通过将DBM拆解为若干个RBM,然后对RBM进行分层的来进行预训练,并将其预训练得到的权重直接赋予DBM的方法。实际上,这只是最经典的训练DBM的方法,近些年诞生了很多直接训练的方法,效果也很不错,现在基本也没有人用预训练了。但是,这种基本思想还是很值得学习的。
本章的主要内容,介绍了四种玻尔兹曼模型的发展,并重点介绍了DBN模型的不足之处(对中间层建模用到一层的参数),从而引出了DBM模型;介绍了DBM模型中的Double counting问题,并对其进行了详细的解释;最后对DBM模型进行了总结,并解释了边界层的处理方法。
实际上DBM模型的演变都非常的Intuitive,不需要太多的数学证明也可以理解。个人觉得这样的思想在科研中很重要,很多情况都是有一个intuitive的想法,然后实验发现确实work,最后寻找证明的方法。(个人愚见)
参考B站视频【机器学习】【白板推导系列】
更多干货,第一时间更新在以下微信公众号:

您的一点点支持,是我后续更多的创造和贡献

转载到请包括本文地址 更详细的转载事宜请参考文章如何转载/引用