任务描述

采用CUDA实现矩阵乘法：A矩阵：1024x1024，B矩阵：1024x1024，C矩阵：1024x1024，目标是尽可能的减少整个流程时间

学习目标

入门cuda,什么是cuda，cuda的基本操作
如何对一个cuda问题，基于cuda领域持续优化，从哪些角度思考，优化cuda需要结合硬件情况，不只是考虑算法的时间复杂度，也需要从硬件是否可以实现甚至实现的高效性考虑，同时也需要上机器评测，部分数值需要实际机器实验佐证
Nsight System安装和使用，工具侧帮助分析算法性能
triton加速https://zhuanlan.zhihu.com/p/697626885

多个版本的优化

cpu版本

CPU版本串行Naive Algorithm（基础版），时间复杂度O(n^3)，

void matrixSerial(float *hostA, float *hostB, float *hostC, int M, int K,
                  int N) {
  for (int i = 0; i < M; i++) {
    for (int j = 0; j < N; j++) {
      float tmp = 0;
      for (int s = 0; s < K; s++) {
        tmp += hostA[i * K + s] * hostB[s * N + j];
      }
      hostC[i * N + j] = tmp;
    }
  }
}

串行CPU算法的优化还有使用矩阵分块理论，能减少常量但是时间复杂度保持不变O(n^3)。另外经典的 Strassen算法是一种基于分治法的优化算法，通过减少乘法次数来降低时间复杂度。时间复杂度为 \(O(n^{log_{2}^{7}})\) 最新nature文章《Discovering faster matrix multiplication algorithms with reinforcement learning》通过强化学习来挖掘出新的矩阵乘法分块策略，类似NAS的思路，开创新的算法研究方向。

GPU版本

多个GPU优化思路版本

v1: 基础版

v2: 共享内存分块

v3: 寄存器分块

v4: 重排索引

v5: float4访存

v6: 解bank冲突

v7: 内积转外积

v8: 双缓冲

v9:cublas

v10: tensor core来优化

第一版本:基础版

优化思路

GPU的计算流程本质是类似map-reduce的处理方式，对矩阵每个元素并发（非并行）计算得到整个矩阵的结果。

代码实现

__global__ void matrixKernal1st(float *dA, float *dB, float *dC, int M, int K,
                                int N) {
  int row = threadIdx.x + blockIdx.x * blockDim.x;
  int col = threadIdx.y + blockIdx.y * blockDim.y;
  float tmp = 0;
  if (row < M && col < N) {
    for (int s = 0; s < K; s++) {
      tmp += dA[row * K + s] * dA[s * N + col];
    }
    dC[row * N + col] = tmp;
  }
}

性能比较

机器	运行参数	GPU use time	kernel time	CPU time	The error between CPU and GPU
单卡A100 显存80G	M-K-N: 1024-1024-1024 GPU use time: 0.5785 second kernel time: 0.0165 second, 16.5047 ms grid dim: 32, 32, 1 block dim: 32, 32, 1 CPU time:3.77 second The error between CPU and GPU: 0.0000e+00	0.5785	0.0165	3.77	0.0000e+00
单卡3090 显存24G	M-K-N: 1024-1024-1024 GPU use time: 0.8050 second kernel time: 0.0087 second, 8.7018 ms grid dim: 32, 32, 1 block dim: 32, 32, 1 CPU time:2.19 second The error between CPU and GPU: 0.0000e+00	0.8050	0.0087	2.19	0.0000e+00

第二版本:共享内存分块

优化思路

share memory的使用

share memory：针对当前线程块所有线程都可见
假设矩阵A,B,C都是6×6的方阵，block_dim=(3.3,1)，grid_dim=(2.2,1)
对于Block(0.0)，设置共享内存数组SA[3][6]和SB[6][3]，将对应矩阵元素从global memory 加载到share memory;
和原来相比，仍然存在重复读取的情况，但是原来重复读取的是global memory，现在重复读取的是share memory
share memory存放的SA形状为[BLOCK_DIM_x,K]，SB形状为[K,BLOCK_DIM_y]，如果K太大如何处理？

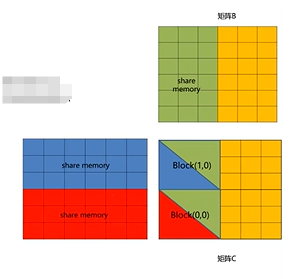
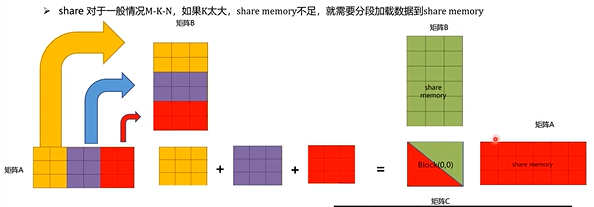
何时使用share memory何时不使用是依据相乘矩阵的尺寸决定

不使用share memory Thread角度：计算一个cij，需要访问global memory的A一行，B一列 Block角度：计算BLOCK_DIM_x * BLOCK_DIM_y个元素，访问global memory次数为BLOCK_DIM_x*BLOCK_DIM_yx(3K)，计算访问比，计算访存比为1/(3K)

使用share memory Thread角度：计算一个cy需要循环K/BLOCK_DIM次，每次循环访问sharememory中SA一行，SB一列 Block角度：计算BLOCK_DIMxBLOCK_DIM个元素需要循环K/BLOCK_DIM次，每次循环访问global memory次数为BLOCK_DIM * BLOCK_DIM * 2，整体访问global memory次数为BLOCK_DIM×BLOCK_DIM×2×K/BLOCK_DIM+BLOCK_DIM×BLOCK_DIM=BLOCK_DIM×(2xK+BLOCK_DIM)，计算访问比，计算访存比为1/(2K/BLOCK_DIM+1)

代码实现

template <int BLOCK_DIM>
__global__ void matrixKernel2nd(float *dA, float *dB, float *dC, int M, int K, int N)
{
    int row = threadIdx.x + blockIdx.x * blockDim.x;
    int col = threadIdx.y + blockIdx.y * blockDim.y;
    float tmp = 0.0f;
    __shared__ float SA[BLOCK_DIM][BLOCK_DIM];
    __shared__ float SB[BLOCK_DIM][BLOCK_DIM];
    int width = (K + BLOCK_DIM - 1) / BLOCK_DIM;
    for (int ph = 0; ph < width; ph++)
    {
        if (row < M && threadIdx.y + ph * BLOCK_DIM < K)
        {
            SA[threadIdx.x][threadIdx.y] = dA[row * K + threadIdx.y + ph * BLOCK_DIM];
        }
        else
        {
            SA[threadIdx.x][threadIdx.y] = 0.0f;
        }
        if (threadIdx.x + ph * BLOCK_DIM < K && col < N)
        {
            SB[threadIdx.x][threadIdx.y] = dB[(threadIdx.x + ph * BLOCK_DIM) * N + col];
        }
        else
        {
            SB[threadIdx.x][threadIdx.y] = 0.0f;
        }
        __syncthreads();
        for (int s = 0; s < BLOCK_DIM; s++)
        {
            tmp += SA[threadIdx.x][s] * SB[s][threadIdx.y];
        }
        __syncthreads();
    }
    if (row < M && col < N)
    {
        dC[row * N + col] = tmp;
    }
}

性能比较

机器	运行参数	GPU use time	kernel time	CPU time	The error between CPU and GPU
单卡A100 显存80G	M-K-N: 1024-1024-1024 GPU use time: 0.3008 second kernel time: 0.0031 second, 3.0668 ms grid dim: 32, 32, 1 block dim: 32, 32, 1 CPU time:3.79 second The error between CPU and GPU: 0.0000e+00	0.5785	0.0165	3.77	0.0000e+00
单卡3090 显存24G	M-K-N: 1024-1024-1024 GPU use time: 0.6995 second kernel time: 0.0035 second, 3.5311 ms grid dim: 32, 32, 1 block dim: 32, 32, 1 CPU time:2.19 second The error between CPU and GPU: 0.0000e+00	0.6995	0.0035	2.19	0.0000e+00

第三版本:寄存器分块

优化思路

引入BM=BLOCK_DIM_x * TM，BN=BLOCK_DIM_y * TN
一个线程块计算矩阵C的元素数目为BMxBN，访问global memory中A,B的数目为BM * K+BN * K，计算量为（BM×BN×K)×2
计算c元素需要循环次数为K/BK，每次循环读取A中BMxBK个元素进入share memory，从B中读取BNxBK个元素进入share memory
BM,BN越大越好，但是share memory有限

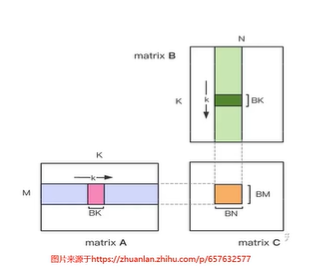
代码实现

template <int BM, int BN, int BK, int TM, int TN>
__global__ void matrixKernel3nd(float *dA, float *dB, float *dC, int M, int K, int N)
{

    int indA = TM * (threadIdx.x + blockIdx.x * blockDim.x);
    int indB = TN * (threadIdx.y + blockIdx.y * blockDim.y);
    float tmp[TM][TN] = {0.0f};
    for (int index_q = 0; index_q < TM; index_q++)
    {
        for (int index_v = 0; index_v < TN; index_v++)
        {
            if (indA + index_q < M && indB + index_v < N)
            {
                for (int s = 0; s < K; s++)
                {
                    tmp[index_q][index_v] += dA[(indA + index_q) * K + s] * dB[s * N + indB + index_v];
                }
            }
        }
    }
    for (int index_q = 0; index_q < TM; index_q++)
    {
        for (int index_v = 0; index_v < TN; index_v++)
        {
            if (indA + index_q < M && indB + index_v < N)
            {
                dC[(indA + index_q) * N + indB + index_v] = tmp[index_q][index_v];
            }
        }
    }
}

性能比较

机器	运行参数	GPU use time	kernel time	CPU time	The error between CPU and GPU
单卡A100 显存80G	M-K-N: 1024-1024-1024 GPU use time: 0.7971 second kernel time: 0.0247 second, 24.6882 ms grid dim: 32, 32, 1 block dim: 32, 32, 1 CPU time:3.78 second The error between CPU and GPU: 0.0000e+00	0.7971	0.0247	3.78	0.0000e+00
单卡3090 显存24G	M-K-N: 1024-1024-1024 GPU use time: 0.8331 second kernel time: 0.0106 second, 10.6388 ms grid dim: 32, 32, 1 block dim: 32, 32, 1 CPU time:2.19 second The error between CPU and GPU: 0.0000e+00	0.8331	0.0106	2.19	0.0000e+00

第四版本:重排索引

优化思路

优化矩阵load至share memory过程

选择blockDim=(32,32,1)，TM=TN=4,BK=8(参考https://zhuanlan.zhihu.com/p/410278370)
SA形状为[128,8]，SB形状为[8,128]，计算得到形状为[128,128]的子矩阵
0≤tid=threadldx.x+threadldx.y*blockDim.x≤1023
smem_a_m(tid%128∈ {0,,127},smem_a_k=tid/128∈ {0,,8}
smem_b_k=tid%8∈{0,…,8},smem_b_k=tid/8∈{0,…,127}
这种做法的特点是：BM * BK=BN * BK=BLOCK_DIM_x * BLOCK_DIM_y，需要重新根据一维线程索引排布为二维索引

代码实现

template <int BM, int BN, int BK, int TM, int TN>
__global__ void matrixKernel4nd(float *dA, float *dB, float *dC, int M, int K, int N)
{
    __shared__ float SA[BM * BK];
    __shared__ float SB[BK * BN];
    int indA = TM * (blockIdx.x * blockDim.x);
    int indB = TN * (blockIdx.y * blockDim.y);
    int width = (K + BK - 1) / BK;
    float tmp[TM * TN] = {0.0f};
    int tid = threadIdx.x + threadIdx.y * blockDim.x;
    int smem_a_m = tid % 128;
    int smem_a_k = tid / 128;
    int smem_b_k = tid % 8;
    int smem_b_n = tid / 8;
    for (int ph = 0; ph < width; ph++)
    {

        if (indA + smem_a_m < M && smem_a_k + ph * BK < K)
        {
            SA[smem_a_m * BK + smem_a_k] = dA[(indA + smem_a_m) * K + smem_a_k + ph * BK];
        }
        else
        {
            SA[smem_a_m * BK + smem_a_k] = 0.0f;
        }
        if (indB + smem_b_n < N && smem_b_k + ph * BK < K)
        {

            SB[smem_b_k * BN + smem_b_n] = dB[(smem_b_k + ph * BK) * N + indB + smem_b_n];
        }
        else
        {
            SB[smem_b_k * BN + smem_b_n] = 0.0f;
        }

        __syncthreads();
        for (int index_q = 0; index_q < TM; index_q++)
        {
            for (int index_v = 0; index_v < TN; index_v++)
            {
                int reg_c_m = threadIdx.x * TM + index_q;
                int reg_c_n = threadIdx.y * TN + index_v;
                for (int index_k = 0; index_k < BK; index_k++)
                {
                    tmp[index_q * TN + index_v] += SA[reg_c_m * BK + index_k] * SB[index_k * BN + reg_c_n];
                }
            }
        }
        __syncthreads();
    }
    for (int index_q = 0; index_q < TM; index_q++)
    {
        for (int index_v = 0; index_v < TN; index_v++)
        {
            int reg_c_m = threadIdx.x * TM + index_q;
            int reg_c_n = threadIdx.y * TN + index_v;
            if (indA + index_q < M && indB + index_v < N)
            {
                dC[(indA + reg_c_m) * N + indB + reg_c_n] = tmp[index_q * TN + index_v];
            }
        }
    }
}

性能比较

机器	运行参数	GPU use time	kernel time	CPU time	The error between CPU and GPU
单卡A100 显存80G	M-K-N: 1024-1024-1024 GPU use time: 0.4615 second kernel time: 0.0091 second, 9.1244 ms grid dim: 32, 32, 1 block dim: 32, 32, 1 CPU time:3.80 second The error between CPU and GPU: 0.0000e+00	0.4615	0.0091	3.80	0.0000e+00
单卡3090 显存24G	M-K-N: 1024-1024-1024 GPU use time: 0.8300 second kernel time: 0.0102 second, 10.1694 ms grid dim: 32, 32, 1 block dim: 32, 32, 1 CPU time:2.19 second The error between CPU and GPU: 0.0000e+00	0.8300	0.0102	2.19	0.0000e+00

第五版本: float4访存

优化思路

float4类型访存

float4是一种内置的数据类型，它连续存储四个float类型的数值，总共占用128位（16字节）的内存空间。借助float4可以连续访存4个浮点元素，提高访存速度，注意内存对齐
选择blockDim=(32,32,1)，TM=TN=4，此时BM=BN=128，使用float4单个线程可以访问4个元素，因此选择BK=32，但是这种时候会导致寄存器爆炸
blockDim=(16,16,1),TM=TN=BK=8
SA形状为[128,8]，SB形状为[8,128]，计算得到形状为[128,128]的子矩阵
0≤tid=threadldx.x+threadldx.y * blockDim.x≤255
smem_a_m=tid/2∈{0…,127},smem_a_k=tid%2 ∈{0,1}
smem_b_k=tid/32 ∈{0…,8},smem_b_k=tid%32 ∈{0,…,32}

代码实现

template <int BM, int BN, int BK, int TM, int TN>
__global__ void matrixKernel5th(float *dA, float *dB, float *dC, int M, int K, int N)
{
    __shared__ float SA[BM * BK * 2];
    __shared__ float SB[BK * BN * 2];
    int indA = TM * (blockIdx.x * blockDim.x);
    int indB = TN * (blockIdx.y * blockDim.y);
    int width = (K + BK - 1) / BK;
    float tmp[TM * TN] = {0.0f};
    int tid = threadIdx.x + threadIdx.y * blockDim.x;
    int smem_a_m = tid / 2;
    int smem_a_k = tid % 2;
    int smem_b_k = tid / 32;
    int smem_b_n = tid % 32;
    float a[4];
    float b[4];
    float com_a[TM];
    float com_b[TN];
    //------------
    int ph = 0;
    (float4 &)a[0] = (float4 &)dA[(indA + smem_a_m) * K + 4 * smem_a_k + ph * BK];
    SA[(4 * smem_a_k) * BM + smem_a_m + ph % 2 * BM * BK] = a[0];
    SA[(4 * smem_a_k + 1) * BM + smem_a_m + ph % 2 * BM * BK] = a[1];
    SA[(4 * smem_a_k + 2) * BM + smem_a_m + ph % 2 * BM * BK] = a[2];
    SA[(4 * smem_a_k + 3) * BM + smem_a_m + ph % 2 * BM * BK] = a[3];
    (float4 &)b[0] = (float4 &)dB[(smem_b_k + ph * BK) * N + indB + 4 * smem_b_n];
    (float4 &)SB[smem_b_k * BN + 4 * smem_b_n] = (float4 &)b[0];

    __syncthreads();

    for (int ph = 1; ph < width; ph++)
    {
        (float4 &)a[0] = (float4 &)dA[(indA + smem_a_m) * K + 4 * smem_a_k + ph * BK];
        (float4 &)b[0] = (float4 &)dB[(smem_b_k + ph * BK) * N + indB + 4 * smem_b_n];

        //-------------
        for (int index_k = 0; index_k < BK; index_k++)
        {
            (float4 &)com_a[0] = (float4 &)SA[index_k * BM + threadIdx.x * TM + (ph - 1) % 2 * BM * BK];
            (float4 &)com_a[4] = (float4 &)SA[index_k * BM + threadIdx.x * TM + 4 + (ph - 1) % 2 * BM * BK];
            (float4 &)com_b[0] = (float4 &)SB[index_k * BN + threadIdx.y * TN + (ph - 1) % 2 * BN * BK];
            (float4 &)com_b[4] = (float4 &)SB[index_k * BN + threadIdx.y * TN + 4 + (ph - 1) % 2 * BN * BK];
            for (int index_q = 0; index_q < TM; index_q++)
            {
                for (int index_v = 0; index_v < TN; index_v++)
                {
                    tmp[index_q * TN + index_v] += com_a[index_q] * com_b[index_v];
                }
            }
        }
        SA[(4 * smem_a_k) * BM + smem_a_m + ph % 2 * BM * BK] = a[0];
        SA[(4 * smem_a_k + 1) * BM + smem_a_m + ph % 2 * BM * BK] = a[1];
        SA[(4 * smem_a_k + 2) * BM + smem_a_m + ph % 2 * BM * BK] = a[2];
        SA[(4 * smem_a_k + 3) * BM + smem_a_m + ph % 2 * BM * BK] = a[3];

        (float4 &)SB[smem_b_k * BN + 4 * smem_b_n + ph % 2 * BN * BK] = (float4 &)b[0];
        __syncthreads();
    }
    //--------------
    ph = width;
    for (int index_k = 0; index_k < BK; index_k++)
    {
        (float4 &)com_a[0] = (float4 &)SA[index_k * BM + threadIdx.x * TM + (ph - 1) % 2 * BM * BK];
        (float4 &)com_a[4] = (float4 &)SA[index_k * BM + threadIdx.x * TM + 4 + (ph - 1) % 2 * BM * BK];
        (float4 &)com_b[0] = (float4 &)SB[index_k * BN + threadIdx.y * TN + (ph - 1) % 2 * BN * BK];
        (float4 &)com_b[4] = (float4 &)SB[index_k * BN + threadIdx.y * TN + 4 + (ph - 1) % 2 * BN * BK];
        for (int index_q = 0; index_q < TM; index_q++)
        {
            for (int index_v = 0; index_v < TN; index_v++)
            {
                tmp[index_q * TN + index_v] += com_a[index_q] * com_b[index_v];
            }
        }
    }
    for (int index_q = 0; index_q < TM; index_q++)
    {
        for (int index_v = 0; index_v < TN; index_v++)
        {
            int reg_c_m = threadIdx.x * TM + index_q;
            int reg_c_n = threadIdx.y * TN + index_v;
            if (indA + index_q < M && indB + index_v < N)
            {
                dC[(indA + reg_c_m) * N + indB + reg_c_n] = tmp[index_q * TN + index_v];
            }
        }
    }
}

性能比较

机器	运行参数	GPU use time	kernel time	CPU time	The error between CPU and GPU
单卡A100 显存80G	M-K-N: 1024-1024-1024 GPU use time: 0.8365 second kernel time: 0.0000 second, 0.0000 ms grid dim: 32, 32, 1 block dim: 32, 32, 1 CPU time:3.83 second The error between CPU and GPU: 1.7090e+03	0.8365	0.0000	3.83	1.7090e+03
单卡3090 显存24G	M-K-N: 1024-1024-1024 GPU use time: 0.6499 second kernel time: 0.0000 second, 0.0000 ms grid dim: 32, 32, 1 block dim: 32, 32, 1 CPU time:2.19 second The error between CPU and GPU: 1.7090e+03	0.6499	0.0000	2.19	1.7090e+03

疑问点：cpu与gpu版本结果不一致

第六版本: 解bank冲突

优化思路

bankconflict

share memory划分为32个Bank，每个Bank的宽度是4Bytes，如果同一个warp的32个线程访问不同Bank，性能最佳，否则就会产生bank conflict
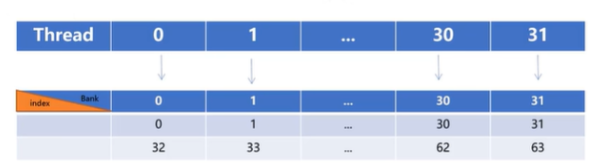
对于固定的线程（threadldx.x,threadldx.y)，计算的c元素索引为 [8xthreadIdx.x+index_q][8xthreadldx.y+index_y]，访问的SA索引为 (8 * threadldx.x+index_q)xBK+index_k=64 * threadldx.x+index_q * 8+index_k，访问的SB索引为 index_k * 128+8 * threadldx.y+indexv，固定index_q和index_v，发现SA的访问存在Bank conflict
对SA的load做一个转置得到[8][128]，这样处理可以避免Bank conflict

代码实现

template <int BM, int BN, int BK, int TM, int TN>
__global__ void matrixKernel6th(float *dA, float *dB, float *dC, int M, int K, int N)
{
    __shared__ float SA[BM * BK * 2];
    __shared__ float SB[BK * BN * 2];
    int indA = TM * (blockIdx.x * blockDim.x);
    int indB = TN * (blockIdx.y * blockDim.y);
    int width = (K + BK - 1) / BK;

    int tid = threadIdx.x + threadIdx.y * blockDim.x;
    int smem_a_m = tid / 2;
    int smem_a_k = tid % 2;
    int smem_b_k = tid / 32;
    int smem_b_n = tid % 32;
    float4 a[1];
    float4 b[1];
    float4 com_a[2];
    float4 com_b[2];
    float4 tmp[16];
    memset(tmp, 0.0f, sizeof(tmp));
    //------------
    int ph = 0;
    (float4 &)a[0] = (float4 &)dA[(indA + smem_a_m) * K + 4 * smem_a_k + ph * BK];
    SA[(4 * smem_a_k) * BM + smem_a_m] = a[0].x;
    SA[(4 * smem_a_k + 1) * BM + smem_a_m] = a[0].y;
    SA[(4 * smem_a_k + 2) * BM + smem_a_m] = a[0].z;
    SA[(4 * smem_a_k + 3) * BM + smem_a_m] = a[0].w;
    (float4 &)b[0] = (float4 &)dB[(smem_b_k + ph * BK) * N + indB + 4 * smem_b_n];
    (float4 &)SB[smem_b_k * BN + 4 * smem_b_n] = (float4 &)b[0];
    for (int id = 0; id < 4; id++)
    {

        if (indB + 4 * smem_b_n + id >= N || smem_b_k + ph * BK >= K)
        {

            SB[smem_b_k * BN + 4 * smem_b_n + id] = 0.0f;
        }
    }
    __syncthreads();

    for (int ph = 1; ph < width; ph++)
    {
        (float4 &)a[0] = (float4 &)dA[(indA + smem_a_m) * K + 4 * smem_a_k + ph * BK];

        (float4 &)b[0] = (float4 &)dB[(smem_b_k + ph * BK) * N + indB + 4 * smem_b_n];

        //-------------
        for (int index_k = 0; index_k < BK; index_k++)
        {
            (float4 &)com_a[0] = (float4 &)SA[index_k * BM + threadIdx.x * TM + (ph - 1) % 2 * BM * BK];
            (float4 &)com_a[1] = (float4 &)SA[index_k * BM + threadIdx.x * TM + 4 + (ph - 1) % 2 * BM * BK];
            (float4 &)com_b[0] = (float4 &)SB[index_k * BN + threadIdx.y * TN + (ph - 1) % 2 * BN * BK];
            (float4 &)com_b[1] = (float4 &)SB[index_k * BN + threadIdx.y * TN + 4 + (ph - 1) % 2 * BN * BK];
            addSpecial4(tmp[0], com_a[0].x, com_b[0]); // index_q = 0, 0<= index_v <= 3
            addSpecial4(tmp[1], com_a[0].x, com_b[1]); // index_q = 0, 4<= index_v <= 7
            addSpecial4(tmp[2], com_a[0].y, com_b[0]); // index_q = 1, 0<= index_v <= 3
            addSpecial4(tmp[3], com_a[0].y, com_b[1]); // index_q = 1, 4<= index_v <= 7
            addSpecial4(tmp[4], com_a[0].z, com_b[0]); // index_q = 2, 0<= index_v <= 3
            addSpecial4(tmp[5], com_a[0].z, com_b[1]); // index_q = 2, 4<= index_v <= 7
            addSpecial4(tmp[6], com_a[0].w, com_b[0]); // index_q = 3, 0<= index_v <= 3
            addSpecial4(tmp[7], com_a[0].w, com_b[1]); // index_q = 3, 4<= index_v <= 7

            addSpecial4(tmp[8], com_a[1].x, com_b[0]);  // index_q = 4, 0<= index_v <= 3
            addSpecial4(tmp[9], com_a[1].x, com_b[1]);  // index_q = 4, 4<= index_v <= 7
            addSpecial4(tmp[10], com_a[1].y, com_b[0]); // index_q =5, 0<= index_v <= 3
            addSpecial4(tmp[11], com_a[1].y, com_b[1]); // index_q = 5, 4<= index_v <= 7
            addSpecial4(tmp[12], com_a[1].z, com_b[0]); // index_q = 6, 0<= index_v <= 3
            addSpecial4(tmp[13], com_a[1].z, com_b[1]); // index_q = 6, 4<= index_v <= 7
            addSpecial4(tmp[14], com_a[1].w, com_b[0]); // index_q =7, 0<= index_v <= 3
            addSpecial4(tmp[15], com_a[1].w, com_b[1]); // index_q = 7, 4<= index_v <= 7
        }
        SA[(4 * smem_a_k) * BM + smem_a_m + ph % 2 * BM * BK] = a[0].x;
        SA[(4 * smem_a_k + 1) * BM + smem_a_m + ph % 2 * BM * BK] = a[0].y;
        SA[(4 * smem_a_k + 2) * BM + smem_a_m + ph % 2 * BM * BK] = a[0].z;
        SA[(4 * smem_a_k + 3) * BM + smem_a_m + ph % 2 * BM * BK] = a[0].w;
        (float4 &)SB[smem_b_k * BN + 4 * smem_b_n + ph % 2 * BN * BK] = (float4 &)b[0];
        __syncthreads();
    }
    //--------------
    ph = width;
    for (int index_k = 0; index_k < BK; index_k++)
    {
        (float4 &)com_a[0] = (float4 &)SA[index_k * BM + threadIdx.x * TM + (ph - 1) % 2 * BM * BK];
        (float4 &)com_a[1] = (float4 &)SA[index_k * BM + threadIdx.x * TM + 4 + (ph - 1) % 2 * BM * BK];
        (float4 &)com_b[0] = (float4 &)SB[index_k * BN + threadIdx.y * TN + (ph - 1) % 2 * BN * BK];
        (float4 &)com_b[1] = (float4 &)SB[index_k * BN + threadIdx.y * TN + 4 + (ph - 1) % 2 * BN * BK];
        addSpecial4(tmp[0], com_a[0].x, com_b[0]); // index_q = 0, 0<= index_v <= 3
        addSpecial4(tmp[1], com_a[0].x, com_b[1]); // index_q = 0, 4<= index_v <= 7
        addSpecial4(tmp[2], com_a[0].y, com_b[0]); // index_q = 1, 0<= index_v <= 3
        addSpecial4(tmp[3], com_a[0].y, com_b[1]); // index_q = 1, 4<= index_v <= 7
        addSpecial4(tmp[4], com_a[0].z, com_b[0]); // index_q = 2, 0<= index_v <= 3
        addSpecial4(tmp[5], com_a[0].z, com_b[1]); // index_q = 2, 4<= index_v <= 7
        addSpecial4(tmp[6], com_a[0].w, com_b[0]); // index_q = 3, 0<= index_v <= 3
        addSpecial4(tmp[7], com_a[0].w, com_b[1]); // index_q = 3, 4<= index_v <= 7

        addSpecial4(tmp[8], com_a[1].x, com_b[0]);  // index_q = 4, 0<= index_v <= 3
        addSpecial4(tmp[9], com_a[1].x, com_b[1]);  // index_q = 4, 4<= index_v <= 7
        addSpecial4(tmp[10], com_a[1].y, com_b[0]); // index_q =5, 0<= index_v <= 3
        addSpecial4(tmp[11], com_a[1].y, com_b[1]); // index_q = 5, 4<= index_v <= 7
        addSpecial4(tmp[12], com_a[1].z, com_b[0]); // index_q = 6, 0<= index_v <= 3
        addSpecial4(tmp[13], com_a[1].z, com_b[1]); // index_q = 6, 4<= index_v <= 7
        addSpecial4(tmp[14], com_a[1].w, com_b[0]); // index_q =7, 0<= index_v <= 3
        addSpecial4(tmp[15], com_a[1].w, com_b[1]); // index_q = 7, 4<= index_v <= 7
    }
    for (int index_q = 0; index_q < TM; index_q++)
    {
        (float4 &)dC[(indA + threadIdx.x * TM + index_q) * N + indB + threadIdx.y * TN] = (float4 &)tmp[2 * index_q];
        (float4 &)dC[(indA + threadIdx.x * TM + index_q) * N + indB + threadIdx.y * TN + 4] = (float4 &)tmp[2 * index_q + 1];
    }
}

性能比较

机器	运行参数	GPU use time	kernel time	CPU time	The error between CPU and GPU
单卡A100 显存80G	M-K-N: 1024-1024-1024 GPU use time: 0.6988 second kernel time: 0.0000 second, 0.0000 ms grid dim: 32, 32, 1 block dim: 32, 32, 1 CPU time:3.81 second The error between CPU and GPU: 1.7090e+03	0.6988	0.0000	3.81	1.7090e+03
单卡3090 显存24G	M-K-N: 1024-1024-1024 GPU use time: 0.6567 second kernel time: 0.0000 second, 0.0001 ms grid dim: 32, 32, 1 block dim: 32, 32, 1 CPU time:2.19 second The error between CPU and GPU: 1.7090e+03	0.6567	0.0000	2.19	1.7090e+03

第七版本: 内积转外积

优化思路

降低sharememory的读取-V7

得到SA[8][128]和SB[8][128]以后，如何优化计算过程？
计算c过程中，同样存在重复读取share memory的问题
此时SA和SB对于index_k是间断的，但是对于index_q和index_v是连续的，借助寄存器内存和float4快速访问share memory
内积一一>外积

cuda入门

将cuda入门相关的概念放到后面，依据前面学习矩阵乘法涉及到的cuda命令，再依次学习cuda基本概念，以练促学，加深学习的深度

内容过多，平移到CUDA编程基础入门系列

参考链接

如何配置visualcode

写CUDA和写好CUDA到底难在哪

CUDA实现矩阵乘法的8种优化策略编程介绍

CUDA编程基础入门系列（持续更新）

采用CUDA实现矩阵乘法

2024年11月

任务描述

学习目标

多个版本的优化

cpu版本

GPU版本

第一版本:基础版

优化思路

代码实现

性能比较

第二版本:共享内存分块

优化思路

代码实现

性能比较

第三版本:寄存器分块

优化思路

代码实现

性能比较

第四版本:重排索引

优化思路

代码实现

性能比较

第五版本: float4访存

优化思路

代码实现

性能比较

第六版本: 解bank冲突

优化思路

代码实现

性能比较

第七版本: 内积转外积

优化思路

cuda入门

参考链接

CATALOG

FEATURED TAGS

FRIENDS